Enclosure: Thomas Jefferson’s Notes on Étienne Bézout’s Cours de Mathématiques, [before April 1815]
Enclosure
Notes on Étienne Bézout’s Cours de Mathématiques
[before Apr. 1815]
To reduce angles observed on an inclined plane to that of the horison. Bezout. trigonom. 320. cours d’Artillerie.
let d.g.i be the plane of the base of a hill, and a.b.c. points on it’s side at different heights.
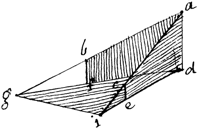 |
° ′ | |
| suppose the ∠b.a.c. found by observation to be | 62–37 | |
| the ∠ of inclination b.a.d (a.d. being vertical) | 88– 5 | |
| the ∠ of inclination of c.a. to wit c.a.d. | 78–17 |
it is required to find the ∠g.d.i. in the plane of the horizon.
let a.b. and a.c be prolonged until they meet the horizontal plane d.g.i. at g. & i.
| consider a.d. as the radius of the tables, | then d.g. & d.i. become tangents of the tables, |
| and a.g. & a.i. their secants; turn to the tables. |
| the ∠g.a.d. | = 88°–5′ has for it’s tabular | secant | 29.90 | neglecting subseqt fractions |
| it’s | tangent | 29.88 | ||
| the ∠i.a.d. | = 78–17 has for it’s tabular | secant | 4.92 | |
| tangent | 4.82 |
1st operation
 |
in the △ a.g.i. given | a.g. = 29.9 |  |
required g.i |
| a.i = 4.92 | ||||
| ∠a = 62°37′1 | ||||
| ag + ai : ag − ai :: ti + g/2 : ti − g/2 = t 49°–43′ | ||||
| then Si. ∠g : ai :: Si. ∠a. : gi = 28. | ||||
2d opern
 |
in the right angled △ a.i.d. | given the ∠a. | = 78°–17′ |
| the hypoth. a.i | = 4.92. reqd d.i. | ||
| Rad. : 4.92 :: Si. 78°–17′ : d.i. = 4.8175 | |||
 |
in the right angled △ a.g.d. | given the ∠a | = 88°–5′ |
| the hypoth. a.g | = 29.9. reqd d.g. | ||
| Rad : 29.9 :: Si. 88°–5′ : d.g. = 29.883 | |||
3d opern
 |
in the △ g.d.i. given | d.g | = 29.883 |  |
required the ∠g.d.i. |
| d.i | = 4.92 | ||||
| g.i | = 28 | ||||
| dg : gi + di :: gi − di : gk − dk = 25.456 | |||||
| and di : Rad. :: kd : Si. ∠dik which is complement to the ∠gdi = 62°–39′–20″2 | |||||
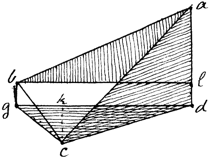 |
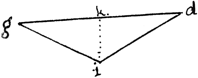
Suppose a the summit of a mountain: ad it’s height, b & c points at it’s foot, c being in the level of it’s base, or of the common horison, & b above that level. |
| ° ′ ″ | ||||
| that the ∠ | aCb | is observed to be | 63–20–40 | |
| Required ad the height of mountn bg the height of station b.3 & the whole △ cdg, being the reduction of the points abc to the plane of the horizon. | aBc | 66–39–20 | ||
| aCd | 7–59–36 | |||
| aBl | 7–48– 0 | |||
| bCg | 0–28–39 | |||
| & that bc is by admeasuremt 6000. feet. | ||||
| we have then the | height of the mountain ad = 1000.f |
| height of the station b. = 50.f. |
| and the whole △ cdg, to wit | Note. the plane of the theodolite
being adjusted to that of the horizon,
will render truly (and without needing reduction)
the horizontal angles at the two stations, whether
they be in the same, or different horizontal planes;
because, if different, as b. and c. their planes being
parallel, the degrees on them will be coincident.
but in this case the base measured on the inclined
plane b.c. must be reduced to the horizontal one g.c. The above diagram supposes the plane of the theodolite adjusted to the inclined plane a.b.c. which renders necessary the reduction of it’s angles as well as lines to the horizontal plane d.g.c. |
|
| cd = 7121.4 | ||
| cg = 5999.8 | ||
| dg = bl = 6935.23 | ||
| ° ′ ″ | ||
| ∠cDg = | 50–30–43 | |
| ∠cGd = | 66–21– 8 | |
| ∠dCg = | 63– 8– 9 | |
MS (MHi); filed with TJ’s Weather Memorandum Book, 1802–16; written entirely in TJ’s hand on both sides of a small sheet; undated, but composed prior to, and probably much earlier than, shipment of TJ’s library to Washington.
TJ based these notes in part on section 320 of Étienne Bézout, Cours de Mathématiques, a l’Usage du Corps Royal de l’Artillerie (Paris, 1788; no. 3681), 1:334–6.
1. Equation interlined.
2. Page ends here.
3. Preceding six words interlined.
Index Entries
- altitude; mathematical source for calculating search
- Bézout, Étienne; Cours de Mathématiques, a l’Usage du Corps Royal de l’Artillerie search
- books; on mathematics search
- Cours de Mathématiques, a l’Usage du Corps Royal de l’Artillerie (É. Bézout) search
- Jefferson, Thomas; Writings; Notes on Étienne Bézout’sCours de Mathématiques search
- mathematics; books on search
- mathematics; trigonometry search
- scientific instruments; theodolites search
- theodolite search

![University of Virginia Press [link will open in a new window] University of Virginia Press](/lib/media/rotunda-white-on-blue.png)
