David Rittenhouse to Thomas Jefferson, 25 June 1790
From David Rittenhouse
Philadelphia June 25th. 1790.
Dr. Sir
Since my last letter (and not before) I have read Mr. Whitehursts Book on the Subject of Measures. Amongst the many different ways of obtaining the Same End, the Method proposed by him seems to be a very good one. I see no reason to object to the lenghth he has assigned from experiments, to a pendulum vibrating seconds in the Latitude of London Vizt. 39.1196 inches.
You Suppose (page 4.) the English foot = 11.pou. 3. lines French. i.e. as 15. to 16. Dr. Maskelyne in the 58 Vol. of Transactions Page 324 States the proportion as 107 to 114, and afterward, page 326, more Correctly as 36. to 38.367.1 If we adopt this, then .0276558 will be a Constant logarithm for reducing English to french measure and the Contrary.
Sir Isaac Newton determines the Earth to be an Oblate Spheroid, having its Axis to the Equatorial diameter as 229 to 230. He then proceeds to shew that the weights of equal Bodies on the Earths surface will be inversely as their distances from the Center and consequently that the lenghths of pendulums vibrating in equal times will be directly as the distance from the Center.2 To determine the distance of any point in an Ellipsis from the Center is not a difficult, but a tedious problem. He therefore judiciously observes that if the difference of the lenghths be taken as the Square of the Lines of the latitude the result will be sufficiently accurate.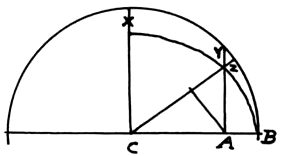 This may be demonstrated thus. Let xC = polar radius, and CB = Equatorial radius. This rad. . x :: Sine Lat. . y = the quantity by which the Sine yA is reduced. But from similarity of Triangles, as rad. . Sine Lat :: y to . . z. The reduction of Cy from the rad that is
This may be demonstrated thus. Let xC = polar radius, and CB = Equatorial radius. This rad. . x :: Sine Lat. . y = the quantity by which the Sine yA is reduced. But from similarity of Triangles, as rad. . Sine Lat :: y to . . z. The reduction of Cy from the rad that is
x × sine/rad = y and sine × y/rad = z therefore x × sine × sine/r = z
and Since the radius and x are both constant z will be as the Square of the Sine of the Lat.
Sir Isaac again says that this reduction of distance from the greatest, or CB will be as the Versed Sine of Double the Latitude, 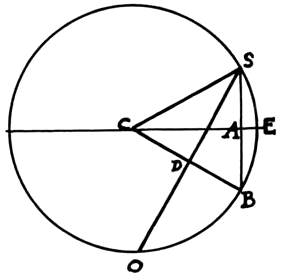 which I thus demonstrate. Let SA be the Sine of the Lat. Make SB double SE. and BO = SB: Thus BD will be the Versed Sine of double the arc of the Latitude. But because the triangles are similar, as rad, or CS . . SA :: 2 SA, or SB . . to BD. But it must be observed that in this Case Newton carries the Versed Sine thro’ the whole diameter of the Circle, so that his Versed Sine of 100.° will be = radius + Sine of 10.°
which I thus demonstrate. Let SA be the Sine of the Lat. Make SB double SE. and BO = SB: Thus BD will be the Versed Sine of double the arc of the Latitude. But because the triangles are similar, as rad, or CS . . SA :: 2 SA, or SB . . to BD. But it must be observed that in this Case Newton carries the Versed Sine thro’ the whole diameter of the Circle, so that his Versed Sine of 100.° will be = radius + Sine of 10.°
| Newtons Table Makes the lenghth of a Second pendulum at the | |||||
| Equator 3 feet 7.468 lines = 36.6223⅓ pouces Log | = | 1.5637460 | |||
| add | .0276553 | ||||
| Equator Pendulum, English, 39.03024 = | 1.5914013 | ||||
| at Lat. 90° = 3 feet. 9.387 lines = 36.78225 pouces Log = | 1.5656383 | ||||
| + | .0276553 | ||||
| English 39.20068 Pendulum at the poles | 1.5932936 | = | |||
| 0.17044 difference for 90.° | |||||
| As the Versed Sine of twice 90° | = | 20,000. | log = | 4.3010300 | |
| To Versed Sine of twice 51.° 31′ | = | 12,255+ | = | 4,0883197 | |
| So is | 17,044 | 4,2315715 | |||
| 8.2859584 | |||||
| to | 10,444 | = | 4,0188612 | ||
| Add to | 39.03024 | Equator pendulum | |||
| Pendulum | 39.13468 for Lat 51.° 31.′ | ||||
| As Versed Sine of twice 90° | = 20,000 Log | = | 4.3010300 |
| to Versed Sine of twice 48.° 50′ | = 11,334+ | = | 4.0543869 |
| So is | 17044 | 4.2315715 | |
| 8.2859584 | |||
| to | .09659 | = | 3.9849284 |
| Add to | 39.03024. | ||
| Pendm. for | 39.12683 Lat. 48.° 50′ | ||
| […] | pendulum for 45.° | is | 39.11546 | Inches |
| do. for 51.° 31′ | = | 39.13468 | ||
| Difference | .01922 | |||
| Pendulum for 45° | = | 39.11546 | ||
| for 48.° 50′ | = | 39.12683 | ||
| Difference | .01137 |
So that I make the differences between the Latitudes for 45°—51.° 31.′ and 48.° 50′ to agree nearly with your differences Viz. .019 and .0112. But I cannot conceive how you make the paris pendulum 39.1923, English measure, if it be 36.71428 french, according to the Bishop of Autun. For if we take the proportion of English to french measure 15 to 16 it will be but 39.1619. But As Maskelyne States the proportion of Measures, only 39.1283.
From the above it appears that Newtons Measure for Lat. 51.° 31′ is greater than that deduced from Experiment by Whitehurst by 15/1000of an inch, and for Lat. 48.° 50′ less than According to the Bishop of Autun by 1½/1000 of an inch. Both differences are inconsiderable, and it is impossible to say whether Whitehursts Experiment was faulty or whether we are mistaken in Supposing the Earths Axis to be to its Equatorial Diameter as 229 to 230.
As soon as I read your mention of Frisi of Milan the name seemed familiar to me, and I was in hopes of finding his Book. But I have only found a printed Account, that a prize on the question of the uniformity of the Earths diurnal Motion, was adjudged by the Petersburg Academy to Paul Frisi professor of Mathematics at Milan. I will endeavour to find it if it be in this City. Would you have me send Emerson or Ferguson or any other Book that is to be had here? Opportunities are not wanting daily by the Stage.
In the Year 1785 Some Experiments were made in England, with all imaginable parade of Accuracy, and recorded in the Philosophical Transactions from which it appears that English plate Brass Expands with 20.° of Fahrenheit 1/4755 part of its whole length. And a Steel rod 1/7862 part. As the difference in our Climate between the greatest Cold in Winter and the greatest heat of Summer cant well be estimated more than 100.° a Steel pendulum will not be liable to vary its lenghth more than 1/2570 part of its whole length, and in Close rooms probably not more than 1/2000 part, making a variation of about 20″ ⅌ Day. This agrees with Newtons Supposition, for the difference of temperature of the Air, within doors in England may be estimated at about 60° of fahrenheit.
I ought perhaps to be more particular about the Comparison of English and French Measures as you may not have the 58th. Vol. of Transactions. Dr. Maskelyne procured from Mr. De La Lande two Iron Copies of the French Toise. Mr. Bird on comparing them found them to differ only 3/1000 of an Inch. A mean of the two measured with the Royal Societies Brass Standard in Temperature of 62° was found to be 76.734 inches, which is the proportion I have taken above.
I intended to have copied the above Scrawl, but thinking that you will find it legible, I hope you will excuse it as it is. I wish it may be in my power to serve you in this or any other matter, tho’ the very bad state of my health [seems] to prevent my promising much. I am, Dear Sir, with great respect and gratitude Your sincere friend & humble Servant,
D. Rittenhouse
RC (DLC); endorsed as received 29 June 1790 and so recorded in SJL.
1. TJ placed an asterisk at this point and then wrote in the margin: “11 po. 3.11 lignes.”
2. TJ bracketed the words “the distance from the center,” interlined “these weights or the gravity of the place,” and then, at top of page and keyed to this point by an asterisk, began the quotation from Newton: “longitudines pendulorum duplicatibus temporibus oscillantium, sunt ut gravitates.”

![University of Virginia Press [link will open in a new window] University of Virginia Press](/lib/media/rotunda-white-on-blue.png)
